Question
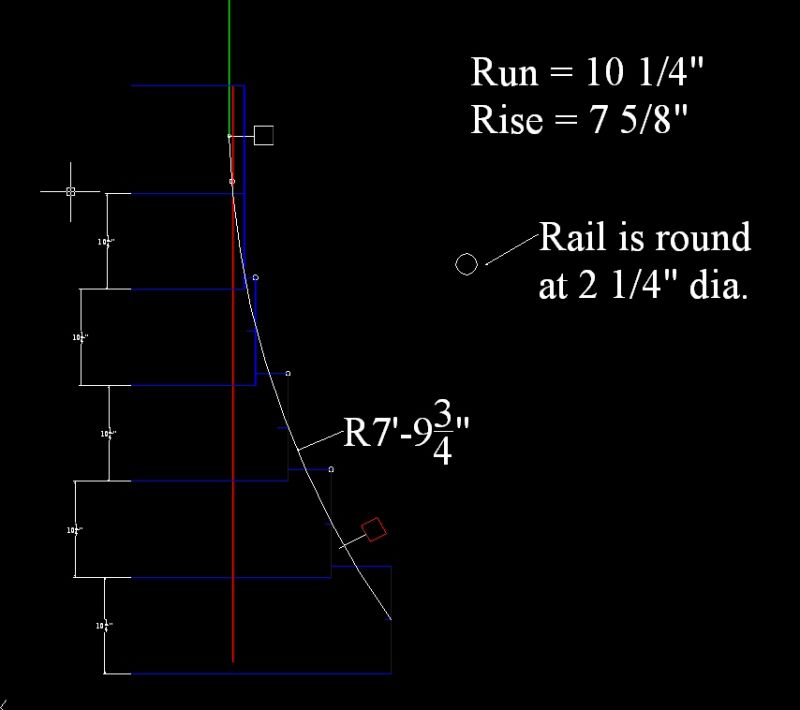
Here's something to chew on. In the attached photo you can see we have a rather straightforward curved stair rail to make. The run of the stairs is 10 1/4" and the rise is 7 5/8". Note: don't be concerned about the gaps between the rail and the tread ends... not my plan!
With most any hand rail, we would just simply build a curved wall and do a glue up of the hand rail laminated strips with the proper rise along the curved wall. I have a theory, though, for this one since, as you'll notice, the hand rail is round at 2 1/4" diameter. My thinking is that unlike a more traditional hand rail profile, where the top surface must always be facing up (hence the twist in the rail created by wrapping the laminations on the curved wall), this perhaps is different.
Since this is a round rail, any "side" can be facing up. So, if I built this on a traditional curved lamination glue up wall, and then profiled it, would it then lay flat on a work surface, or would there be a helix twist in the length of the rail, preventing the rail from laying flat in a single plane?
Trying to picture it I think it would have a helix twist and not lay flat. However, part of me also thinks that I could make this without the curved wall. That is, calculate a stretched out radius from the plan view radius of 93 3/4" and the rise of 7 5/8" along the full run of the curve. If this is the case then I could use that extended radius to just make a single plane eyebrow curve that could be tilted into place. Remember, there is no up on the hand rail profile, so the twist to keep the top edge up isn't an issue... Any "edge" can be up.
Forum Responses
(Architectural Woodworking Forum)
From contributor M:
Lay any curved stair rail on the floor and you'll see that it won't lay flat. So unfortunately, you'll still have to do it the old fashioned way. Also, even though the profile is simpler that a traditional hand rail, I think profiling it will be harder, since there is no "bottom" to index off.
However, in this real world, if you are doing a short enough segment of arc - maybe 3-4 treads or less - you can probably do a flat curve and be done with it. Therefore the helical rail would not be needed.
At what point does the flat curve no longer work? I don't know. How can you predict it? I don't know. How do you calculate the flat curve radius to work on the pitch? I don't know. Am I much help? No. You need a better mathematician than I, plus a good 3D CAD drawing.
I think I have to agree that this is not the right way to do this. However, this is a temporary railing for getting some wedding pictures done and then this entire curved end of the staircase will get redesigned. Go figure!
Next, I did a best fit radius to the helix that was projected onto the plane. I get a radius of 147.31 with a max deviation of .003. Pretty darn good. So, if you could live with making the rail in a bunch of sections that are .319 from flat, you could just round profile them with a 147 in rad on your stock. Pretty standard process for you. I am not sure if that is what you wanted for info. I can provide you with other numbers if you wish.
We do this by breaking the 2 1/4" thickness into 2 layers 1 1/8" each. Segments in each layer are butt jointed together and then the 2 layers are glued together while offsetting all butt joints by half the segment lengths. Makes for a rock solid girder like rail.
Is it easy for you to determine the out of plane rise for the entire radius section of the rail? I have very little experience with 3D drawing. Don't even know if it's something I can do in AutoCAD LT.
When you glue your two halves together, maybe you could deflect the glue-up by the 1.00 dim. Even with spring back it may buy you what you are looking for. Since it is a round profile it will be very forgiving to the eye.
I think they can live with the 1" deviation since it is going to be temporary. Doing it in a single plane like this will cut the price more than in half, so I suspect that would be acceptable. I will contact the customer to discuss your results.
We really couldn't do anything about forcing an out of plane deviation during lamination of the two 1 1/8" thick layers. The butt joints, designed to hold until the layers are brought together, would never take that kind of stress. I'm moving forward here, thanks to your time and help! It is very much appreciated.
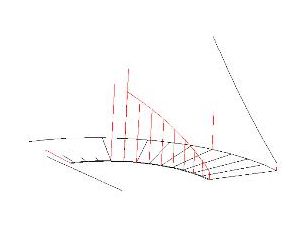
Even the most complex helical curves can be reduced to single-plane bends and then combined to yield sweeping rails and graceful geometric transitions. This forms the basis of the study of "Tangent Handrailing from Single Plane Developments." You can read about it in some very old reprinted books and at least one newer one.
Moulded wood handrails start with the same single plane layout, but the twist and profile must be cut into the curve. These tangent made rails usually follow true helical paths but their graceful curves are the result of the single plane.
I probably have confused a few of you here, but I am not making this stuff up. The math for determining simple helical curvature was first published in the 1750's and is found on this website. It works and it's all you'll need to lay out full round railing pieces that can approximate the true helix. Moulded handrailing and complex helical forms, however, will require a knowledge of tangent handrailing.