Learning Complex Handrail Concepts

Here's a great conversation where an advanced woodworker sits down with a beginner to walk him through some complicated, old-school curved carpentry and joinery. October 3, 2011

Question
I've been attempting to teach myself tangent handrailing. Level to rake fitting have been successful, inclined to inclined has completely evaded me. DiCristina's book, while it’s called “A Simplified Guide”, the drawings make no sense to me. The closest thing I've found is a chapter in Mowat's book called “Elementary Principles of the Cylindric System.” It shows a handrail over a 1/4 circle. Above the plan view is the elliptical drawing. My understanding is that the shaded portion up to O1 is the rise, the line from O1 to M1 is the major axis. How is that length determined, and what is the minor axis?

Forum Responses
(Architectural Woodworking Forum)
From contributor J:
The line you're referring to is the minor axis (or one half of the minor axis). It is always the level line or "ordinate". It is projected from the plan into the elevation and is then used to draw the major axis (which is always drawn 90 degrees to it).

W&A Mowat brothers were English academy science masters, cir.1900 (and not woodworkers). Their stuff is typically harder to understand than your Di Christina book. I suggest you go back to it and start with "The Cardboard Model" (plate 31). Copy it or draw it out on poster board and cut and fold it per instructions.

The lines with the big O (both in plan and elevation) are the ordinate lines (or one half of the minor axis to the curve). The ordinate is always a level line and your reference indicator. It's length in the plan projection and tangent drawing (as well as any lines drawn parallel to it) will always be the same as they are in the plan view. I know I've lost you already but until you do at least one cut-out you will be thrashing about. As you progress, I suggest a separate cut-out for all the various tangent plans. (Di Christina himself made wood block models).

If you prefer the Mowat book than I suggest you skip forward to chapter 14 and work with Fig. 223-5. Don't try to understand it all but just go through it bit by bit and re-draw it all half scale. After that you can use your face-mold template and begin practicing with some soft wood. All this stuff use to be part of a regular woodworkers' apprenticeship but is now considered obsolete. It still works though and can be fun.


From the original questioner:
I'm almost embarrassed to say that I've done the cardboard cutout. I've even done wooden models. Although I can visualize the end result and could produce a "reasonable" result using the Ham and Egg approach I simply have not been able to follow the drawings. I know what it should look like but the drawings don't seem to help in the actual drawing of the fitting. However being pigheaded and stubborn I'll get out my DiCristina book again. Maybe holding it upside down will be better.

From contributor J:
Let's start with plate 68 in the DC book. Everything that you need to see is on this page.

From the original questioner:
Plate 68 starts by referring to plate 53 to obtain the angle of the inclined tangents. In figure 1 it appears the various arcs drawn are to find point G. The line EG is drawn, I'm assuming to locate one end of the fitting, but how if point E determined?

From contributor J:
Are we on the same page?


Click here for higher quality, full size image


From the original questioner:
Yes, that is the same plate. My understanding is that CD is the rise and OC the radius. I see how point F is obtained. What is unclear is how point E is derived. Looking at the dotted outline it seems to be the tangent of the center-line, but how is it found without the dotted drawing.

From contributor J:
E is the vertex of the two tangent planes. Its height is determined by the unfolding of the tangent lines from the plan into the elevation (which is superimposed over the stretch-out or roll-out of the stairs (see plate 27). In this case, the two pitches of the tangent planes are identical which yields a straight pitched line and a true helical handrail segment (see plate 106, fig 2 for an isometric view). In this drawing "B" is the vertex corresponding to E plate 68.

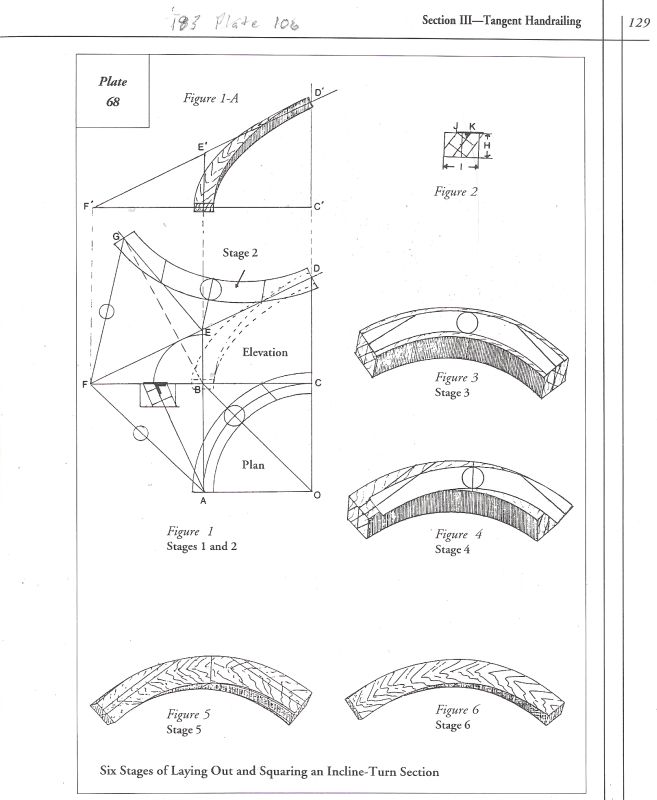
If you're confused just keep going - it will become clear. I suggest that you reproduce this complete set of drawings starting with the plan view. Make the center line radius equal 9.5" Include one straight 10" tread above and below the quarter circle. The quarter circle will contain two winders, making four steps total. This should help you understand how this handrail fits over the stair.


From the original questioner:
Following the drawing in plate 53 it appears that point E is found by being the only point along the extended line AB where an arc will pass through both points F and G. It would seem there is a better approach to locate point E than trial and error. The drawing shows the arc but does not describe how the center point is located.

From contributor J:
I am away from my desk for a few days and without the book but point E is never determined by any kind of trial and error. The height of point E (the vertex of the two tangent planes) determines the classification or type of tangent plan. It will also determine the actual pitch of the plank as well as the joint bevels. Everything is therefore predicated upon the proper height of point E.

In plan view, plate 68 fig 1, imagine a riser and starting point at A and another along line BO and the last at C. Can you see then in the unfolded elevation that BE = one riser and CD = two risers?

If we were to move point E (either up or down) we would change the pitch of both tangent lines FE and ED. This is what makes it possible for a curved handrail to change its pitch from one end to the other within a single oblique plane. I'll check plate 53 in a day or two.


From contributor B:
Point E (plate 53 fig. 1) is indeed an extension of the plan tangent line AB but its height was determined elsewhere is not the subject of this instruction page. This plate is only concerned with the determination of the true "angle of tangents" from the floor plan. The center of arc AF is B and is the rotation of the horizontal tangent line AB into the vertical plane. The center of arc FG is E and is the true tangent length FE rotated until it intersects a 90 degree line drawn from B. The resultant angle GED is now the true angle of the horizontal tangent ABC.

The two other arcs on the drawing originating from C and then D are just another way to locate G. This whole plate shows the three possible tangent plans with equal pitches along with their true tangent angles. When studying these drawings, you really have to jump back and forth from the written instructions to the drawing and identify every line and point as you go.

Related Articles