Para hacer un cono, obviamente necesitas envolver una hoja con forma de Pac-man de lo que sea que estés usando. Las incógnitas son el radio y el tamaño de la cuña que falta. Imagínate un vaso de papel.
Primero, el radio de la hoja es la longitud del cono a lo largo de la costura.
Luego, la circunferencia alrededor de la base (extremo grande) de su cono es la distancia alrededor de la hoja. Lo que queda (esta distancia será menor que la circunferencia del círculo que acabas de dibujar) es la forma de cuña.
Somos un pequeño fabricante de cocinas a medida, con unos 66 empleados. Tenemos una división separada, Keener Architectural Millwork, que está creciendo rápidamente y estamos haciendo cada vez más cosas fuera de lo común. Empezamos haciendo muchas instalaciones médicas y bancos y ahora escuelas enteras y salas de exposición de automóviles nuevos.
Altura inclinada s =
Esto es lo que se me ocurrió:
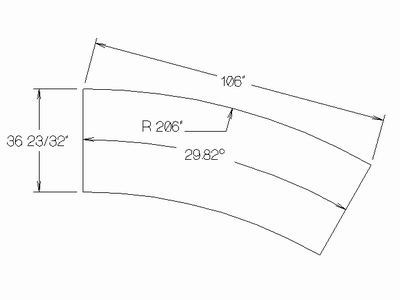
PD:
Confirma el ángulo matemáticamente con
2*arcsen(acorde/dia) =
2 arcosen(106/412) = 29.81764
*Creo* que este es el desarrollo correcto de tu cono. Quizás alguien más publique el suyo. No tengo mi calculadora de ciencias ni mis ecuaciones aquí, por lo que los números no son exactos. Lo dibujé rápidamente en el CAD de mi casa.
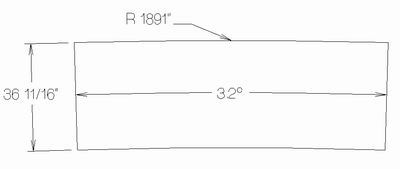
Primero encuentre la altura total del cono *lleno* usando CAD o triángulos similares:
(triángulos semejantes)
usando a^2 + b^2 = c^2 podemos obtener la longitud 'a lo largo' del cono
206^2 + 1879,75^2 = longitud^2
el círculo que acabas de crear tiene una circunferencia de:
Tu piel debe tener extremos en ángulo (la forma de pastel):
ángulo/360=1294,3/11881,3
ángulo = 39,2 grados
Utilice un 'pastel' de 39,2 grados fuera de su círculo y esa será su piel. Puedes compensar tu círculo para una pared que no sea el cono completo. En tu caso:
36,5^2 + 4^2 = desplazamiento^2
No creo que la longitud de la cuerda sea útil para hacer revestimientos más que para estimar las uniones o el número de paneles. Será necesario ajustar ambos extremos a mano, a menos que la pared termine en un verdadero corte "a lo largo" del cono (es decir, lo mismo que una junta de panel, lo cual es poco probable).
Entonces, al observar la relación entre una copa tridimensional y una copa aplanada bidimensional, puedo ver que el ángulo de la pendiente cambia. La longitud de la cuerda cambiaría el ángulo de la pieza necesaria para laminar un objeto que es menos de la mitad de un cono aplanado. No veo una relación inmediata entre el radio de un cono y el radio de un cono aplanado.
Con un poco de investigación, encontraré algunas fórmulas para crear un archivo de Excel para resolver esto.
?
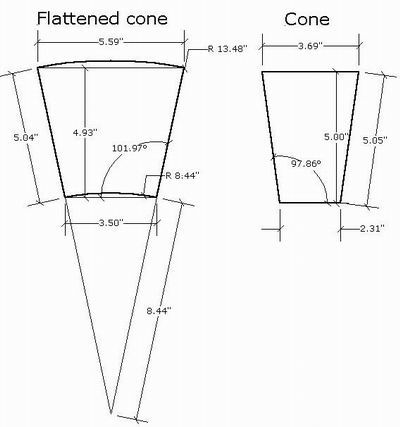
Si tienes la longitud de una cuerda y el radio de un cono, necesitas encontrar la longitud del arco para eso.
Calcula el radio multiplicado por pi, divídelo por 2. Esto es la mitad de la circunferencia. Ahora resta la longitud del arco de tu cono parcial del número de la media circunferencia. Usa la mitad de la respuesta para compensar las líneas del dibujo del cono aplanado. (Las líneas discontinuas en el dibujo representan esto). Esta debería ser la pieza de material que envolverá un cono parcial.
View full size image
Utilice Autodesk Inventor 6. Lo dibujará de la forma que desee y lo distribuirá de forma plana. No se requieren fórmulas.
Los comentarios a continuación se agregaron después de que esta discusión del foro se archivara como un artículo de la base de conocimientos (add your comment).
Del colaborador A:
El colaborador M tiene razón:
la longitud del lado de 3,2 grados es 36,7185. Para diseñar sin CAD, haga esto:
3) Haz un arco que conecte estos 2 puntos con el centro. Este será tu arco superior.
6) Dibuja un arco que pase por estos 3 puntos. Esto te dará el radio de 102 para la parte inferior del cono.